Excelでモンテカルロシミュレーションなどを行う場合、乱数を発生させてシミュレーションを行いますが、その乱数はシミュレーションで想定する確率分布に従うように発生させる必要があります。例えば正規分布に従って生じる金融市場の動き(上下の変化)などです。このようなある確率分布に従う乱数を簡単に取得する方法である逆関数法について簡単にまとめます。Excelを用いて実際に乱数を生成させる方法についてはこちらをご参照ください。
逆関数法に必要なもの
まず逆関数法を用いて、ある確率分布(正規分布など)に従う乱数を発生させるには
- 一様乱数(0~1の間の値を均一な確率で取る乱数)
- 確率分布の累積分布関数の逆関数
の2つが必要です。
累積分布関数
累積分布関数とは「ある確率分布に従う変数が、ある値よりも小さい値を取る確率」の値を取る関数です。わかりにくいですね。
正規分布を例に考えると、累積分布関数は横軸の値(X)を与えると下記グラフの赤色部分の面積を値として取る関数です(グラフの縦軸は確率です)。
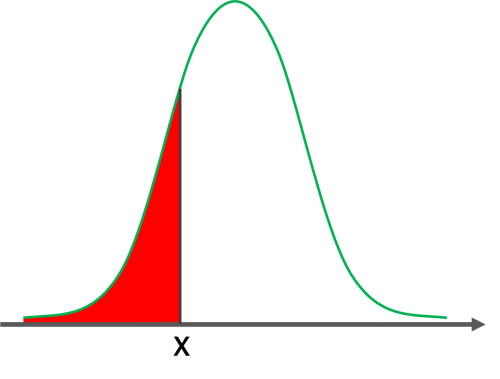
累積分布関数の性質としては今頭に入れておくべきことは、
- 単調増加関数(横軸の値が右に動くと、面積は単調に増加する)
- 値は0~1を取る(確率なので)
という点です。数学的証明をしたいわけではないので、厳密な言い方ではないですが、「値として0~1をとる単調増加関数なので、縦軸の値と横軸の値が1対1対応」します。値が1対1対応しているので、0~1の確率を指定してやれば、逆に横軸の値も確定します。この「確率(0~1)⇒横軸の値」を与える関数を累積分布関数の逆関数と呼びます。出力される横軸の値がどれぐらいの頻度で生じるかはもともとの確率分布に従います。
一様乱数⇒逆関数⇒目的の乱数
ここまで説明すると大体わかってきたかと思いますが、逆関数法は「ランダムに発生する0~1の値を累積分布関数の逆関数に与えてやることにより、元々の確率分布に従う値を発生させる方法」になります。
簡略化して書くと
「一様乱数(0~1)⇒ 逆関数 ⇒ 確率分布に従う乱数」
という関係性から目的の乱数を生成する方法です。
エクセルでは備え付けの関数として一様乱数(0~1)を発生させる「Rand()」という関数が存在します。このRand関数を使って生成した一様乱数を累積分布関数の逆関数に引数として与えてやれば、目的の乱数が生成できます。
